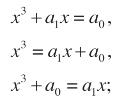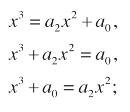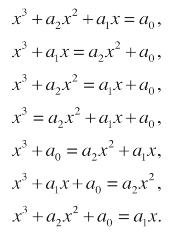di Piero Giuseppe Goletto
Già Al-Khuwarizmi distingueva sei tipi di equazioni di primo e secondo grado:
- quadrati uguali a radici: x 2 = x,
- quadrati uguali a numeri: x 2 = a,
- radici uguali a numeri: x = a,
- quadrati e radici uguali a numeri: x 2 + ax = b,
- quadrati e numeri uguali a radici: x 2 + a = bx,
- quadrati uguali a radici e numeri: x \ = ax + b
che ci pervennero tra l’altro attraverso i libri di Luca Pacioli. La scoperta della procedura per la risoluzione delle equazioni di terzo grado vede in primo piano la figura di Girolamo Cardano. Medico e matematico, non era personaggio di buon carattere e non ebbe vita fortunata.
Cardano divenne celebre per aver trovato le formule risolutive per le equazioni di terzo grado che appaiono per la prima volta nell’Ars Magna del 1545. A questa pubblicazione è legata una grossa controversia.

Infatti, altri matematici riuscirono nello stesso periodo a trovare le risoluzioni per taluni tipi di equazioni cubiche. Ci riferiamo soprattutto al Tartaglia, noto anche per il “triangolo”

Cardano convince Tartaglia a rivelargli tali procedimenti promettendogli di mantenere il segreto.
Nell’Ars Magna, Cardano pubblica le formule risolutive per le equazioni di terzo grado trovate da Tartaglia, le relative dimostrazioni e le soluzioni per tutte le equazioni di terzo grado.
Nel XVI secolo un matematico per acquisire fama sfidava un suo collega a risolvere un problema da lui proposto. Nella circostanza specifica era stata organizzata una sfida tra Antonio Maria Fior e il Tartaglia. Oggetto della sfida era un problema la cui soluzione era costituita da un’equazione di terzo grado. Tartaglia trovò la soluzione ma tenne per sé, gelosamente nascosta, la regola. Cardano – che insegnava a Bologna – era un’autorità ma non si comportò in modo corretto e pubblicò tale formula. Tartaglia non perdonò mai Cardano al punto che rimasero memorabili le disfide tra i due. Si tenga anche conto che all’epoca il sistema di notazione algebrica non era bene sviluppato, come è oggi; pertanto una formula che oggi apparirebbe ovvia era accessibile solo a pochi esperti.